Subject of Study

選択的不感化ニューラルネット（SDNN）とその応用

背景

深層学習の課題

近年のAI技術の中心である深層学習には，いくつかの技術的課題があります．一つは，訓練用に大量のデータが必要ということです．データを集めている間に問題の性質が時間的に変化する（コンセプトドリフト），あるいは適用する対象（例えば個人）ごとの差が大きいと，必要なデータが十分に得られない場合があります．実際，あまり表には出てきませんが，深層学習がうまくいかない問題というのも少なくありません．

もう一つの大きな課題は，判断根拠が説明されない「ブラックボックス」であるということです．深層学習で用いられる深層ニューラルネット（DNN）は入力から出力までの計算過程が複雑で，なぜそのような判断をしたのか解析するのは容易でありません．これに関しては様々な研究がなされていますが，基本的に入力を振ったときの出力の変化から根拠を推定するものがほとんどで，実際にDNNがその根拠に基づいて判断しているという保証はありません．

浅層ニューラルネット

DNNでは入力層と出力層の間に多数の中間層があり，それらの中間層でも学習を行いますが，これに対して層の数が少なく，学習を行うのは基本的に1層のみであるものを浅層ニューラルネット（SNN）と呼びます． SNNの最も基本的なものは単純パーセプトロンですが，一つの単純パーセプトロンは，入力空間を超平面で線形分離することしかできないため，複雑な問題には使えません（歴史的には，これを解決するために多層化が行われました）．

実用的なSNNの代表例は，サポートベクターマシン（SVM）です．線形のSVMは単純パーセプトロンと同様，線形分離しかできませんが，通常はカーネルによる非線形変換を施すので，元の入力空間では複雑な分類が可能です．但し，非線形カーネルには様々な種類があり，また各カーネルにはいくつかのパラメータがあり，それらによって性能がかなり変わるため，必ずしも使いやすくありません．また，非線形カーネルを通すことにより，どの入力特徴（入力ベクトルの成分）が結果にどのように寄与したのか解析がしづらくなり，透明性が低下する点も問題です．

層の浅さによる透明性の高さや使いやすさを残しつつ，学習能力を高めたSNNはこれまでありませんでした．我々が考案した選択的不感化ニューラルネット（SDNN）は，この問題を解決したものです．

研究の経緯

SNNの一つに，多数の単純パーセプトロンを並列化し，その出力の合計値や多数決で最終的な出力を決める並列パーセプトロンというものがあります．これにより，理論的には多層パーセプトロンと同じだけの表現能力が得られますが，実際に複雑な問題を学習させてもうまくいかないので実用的なモデルではありません．ただ，小脳のパーセプトロンモデルのように，パーセプトロンの学習は人間の脳でも行われている可能性があります（逆に，深層学習や課題に応じたカーネル選択が脳で行われているとは考えられていません）．

我々は，計算論的な考察と脳のモデル化の研究[1-5]などを通じて，入力ベクトルにある操作を施してからパーセプトロンに入力すると，一つのパーセプトロンでかなり複雑な分類問題を学習可能になることを明らかにしました．これを並列化すると，学習能力がさらに高まる上に，脳の海馬の構造とよく整合します．SDNNはこうした研究の結果生まれました．

SDNNの仕組みと特徴

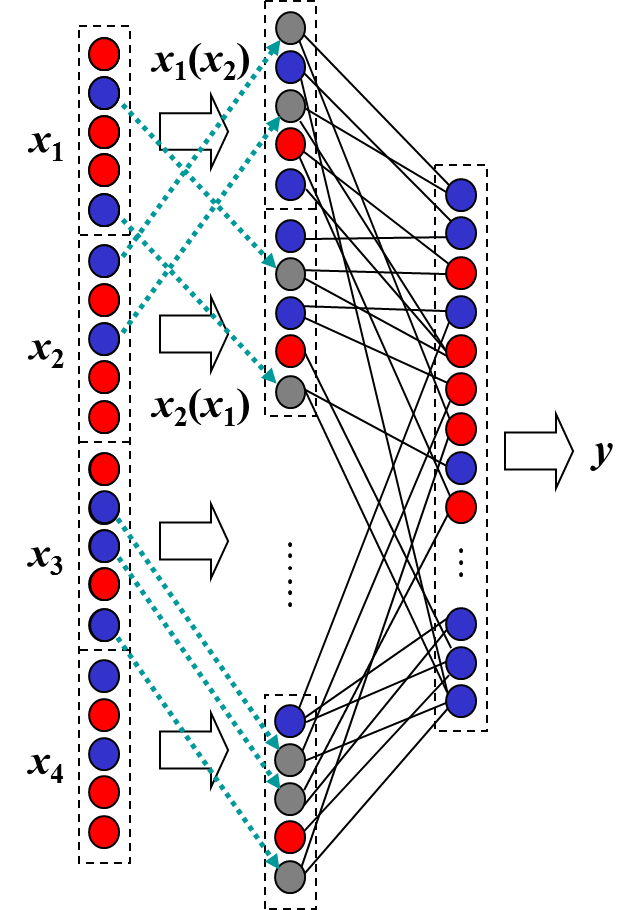図1　SDNNの構造

構造と動作

標準的なSDNNは図1のような構造をしています（例として，入力が4次元の場合を示しています）．入力ベクトルの成分（特徴量）は一般にアナログ値ですが，最初にこれを一定の規則に従って高次元の2値（±1）パターンに変換します．この変換をパターンコーディングと呼びますが，この操作は表引きにより簡単に実現できます．

次に，このパターンを二つずつ，一方が他方を修飾する形で統合します．具体的に，アナログの特徴量x₁, x₂, x₃, x₄を変換したパターンをX₁, X₂, X₃, X₄としたとき，X_iをX_jで修飾することによってX_ij というパターンを得ます．このパターンは，X_iの一部（通常は半数）の成分が0（中立値）となった3値パターンです．成分の一部を0にすることを「選択的不感化」といい，どの成分を0にするかはX_jに依存して決まります．最も単純には，X_iとX_jの成分をランダムに対応付け，対応するX_jの成分が-1のとき0にします．例えば，X_i =(1,1,1,1,-1,-1,-1,-1), X_j =(1,-1,1,-1,1,-1,1,-1) で，仮に同じ位置の成分同士が対応しているならば，X_ij = (1,0,1,0,-1,0,-1,0) となります．同様に，X_j をX_i で修飾すると，X_ji =(1,-1,1,-1,0,0,0,0) が得られます．

最後に，こうして得られた4x3=12個のパターンを並列パーセプトロンへの入力とします．並列するパーセプトロンの出力値の総和に応じて最終的な出力値が決まります．これが正解に一致するように学習しますが，学習によって修正されるのは，いくつかの単純パーセプトロンの出力素子への結合だけです．このように，SDNNの計算は（いくつか注意点がありますが）簡単で，学習も単純で非常に高速です．

動作例

図2は，2変数関数を学習させた例です[6]． (a)が元の関数（正解）で，点(x, y)における関数値が色で表されています．そこから(b)に示す点をサンプリングしてSDNNに与えます．黒塗りの領域にはサンプルがないことに注意して下さい．(c)は学習後のSDNNの出力です．1サンプルあたり数回の学習しかしていませんが，サンプルのない領域を含めて，元の関数がかなりよく再現されていることがわかります．深層学習で同様の結果を出すには，層の数および学習回数をかなり増やす必要があります．

図2　SDNNによる関数近似の例

学習能力

SDNNの出力層は並列パーセプトロンなので，理論上は万能（十分な素子数があれば，任意の連続関数を高精度で表現可能）ですが，実際のサンプル学習能力も非常に高く，ほとんどの場合，学習誤差はきわめて小さくなります．関数は連続である必要はなく，図2の中央部分のように，不連続に変化する部分があっても精度よく近似可能です．

また，図2からわかるように，サンプルが与えられない部分にも学習した結果が及びます．一般に汎化能力と表現能力は相反すると考えられていますが，それは過剰適合（表現能力を高めて学習誤差を減らすと，サンプルのみに適合することによってかえって汎化誤差が増加する現象）が生じるからです．SDNNでは中間層の学習を行わず，個々のパーセプトロンは線形分離しかしないため，過剰適合はほとんど生じません．過剰な素子は使われないか同じ働きをするだけなので，素子数を増やすことによって，汎化能力を低下させることなく表現能力を高めることが可能です．

使いやすさ

SDNNの計算コストは入力次元の2乗に比例して増加するので，入力次元が50～100を超えると実用的ではありません．したがって，DNNのように画像や生のデータをそのまま入力するのではなく，ある程度の特徴抽出を行ってから入力する必要があります．しかし，そのような使用を前提とすれば，以下のような特徴からかなり使いやすいと思います．

まず，入力次元があまり大きくなければ，計算コストが低く学習も早いのでノートPCでも動作します．また，ハイパーパラメータが少なく性能への影響も少ないので，さまざまな設定を試行錯誤的に試す必要がありません．

特徴抽出はしないといけませんが，無効特徴（出力に関係しない入力変数）の影響を受けにくい[7]ので，学習に必要な特徴量が含まれていれば，不要な特徴量を取り除く必要はありません．また，ある限られた場合にのみ有効な特徴を積極的に取り入れることが可能です．

さらに，オンライン追加学習が容易という特徴もあります．多くの学習器では，学習後に新たなデータが追加された場合，古いデータを含めて再学習しなければなりません．新しいデータだけを追加で学習すると，その影響が広範に及んでそれまでの学習結果が大きく崩れてしまうからです（カタストロフィック干渉）．これに対してSDNNでは，新しいサンプルを追加学習したとき，限られた結合荷重しか修正されず，（狭い領域に多くのサンプルが与えられた場合を除いて）その影響は近傍にしか及びません．そのため，古いサンプルの再学習をすることなく，サンプルを1つずつオンラインで学習することが可能です．

一般的な機械学習ツールでは用意されていない操作を含むので，プログラム開発が難しいという問題がありますが，言語によってはライブラリが利用可能です．

透明性

SDNNの最大の特徴は，透明性の高さです．これは，学習層が1層のみであることに加えて，各入力変数（特徴量）の経路が明確に分かれていることによります．

これにより，線形モデルと同様に，あるサンプルに対する出力結果に，どの特徴量がどれだけ影響したかは，その特徴量に関係する部分からの信号の荷重和によって定量的にわかります．また，全体としてどの特徴量が重要でどれが無効かも，その特徴量に関係する部分からの結合荷重の分散から判断できます[8]．

さらに，線形モデルとは違って，特徴量の組合せごとに，出力への寄与や有効性がわかる点も重要な特徴です．単独ではあまり役に立たなくても，別の特徴と組み合わせると非常に有益であることもありますし，このような組合せを考えることによって判断の説明性も大きく高まります．

SDNNの応用

連続状態空間における強化学習

状態変数が連続的な値をとるときには，価値関数を関数近似器で近似する必要がありますが，深層学習などはオンラインでの逐次学習に向かないので，通常は放射状基底関数などの局所的な基底関数を用いて補間する手法が用いられます．しかし，この方法だと汎化が局所的にしか起きないので，離散化して表引きするのとあまり変わらず，多くの学習回数が必要です．また，無効な状態変数が含まれていると学習効率がさらに低下してしまいます．

これに対して，SDNNはオンライン学習に適している上に無効変数の影響を受けにくく大域的な汎化も生じます．そのため，価値関数の近似器として非常に優れており，複雑なアルゴリズムを用いることなく学習効率を向上が期待できます[9-11]．

筋電からの動作推定

表面筋電位信号は，個人差が大きく，電極を貼る位置の微妙な違いによっても変わります．また，例えば手首をひねるような動作の場合，筋電信号と動作の種類や速度との関係は複雑なものになります． SDNNを用いることによって，少数のサンプルを取得してその場ですぐ学習し，動作の種類や動作速度の推定を行う手法を開発しました [12-15].

時系列予測

過去の時系列から将来の値を予測する手法はいろいろありますが，予測対象の性質が時間的に変化するコンセプトドリフト課題に対してはあまりよい性能が得られません．SDNNは逐次追加学習によって対象の変化に追従することができるので，課題によっては既存手法よりも予測誤差が小さくなります[16,17]．

医療情報等の分析

医用画像の認識などで深層学習が優れた結果をだしていますが，判断根拠が不明のため使いにくいという問題があります．SDNNは画像認識には向きませんが，数十個以下の医療情報（検査項目など）から判断する場合に，判断根拠が明確で人間に理解しやすいという特徴があります．今後，この特徴を生かした分析や診断システムへの応用を進める予定です．

脳波解析とうつ病の早期発見

深層学習などを用いた既存研究でうつ病患者と健常者を脳波により判別することはできていますが，うつ病に伴う認知機能の低下に基づいて判断していると考えられ，うつ病の兆候を捉えることには成功していません．これに対して我々は，SDNNを用いて脳波を解析し，脳内の情報の流れを個人ごとに捉えるという手法を開発し，これを用いてうつ病の早期発見につながる脳活動を捉えようとしています．